How do I solve Queens on LinkedIn?
I’m glad you asked. I can usually solve the daily puzzle in a minute or two. Here’s what I do.
(I do play with Auto-place Xs. It’s a huge time saver.)
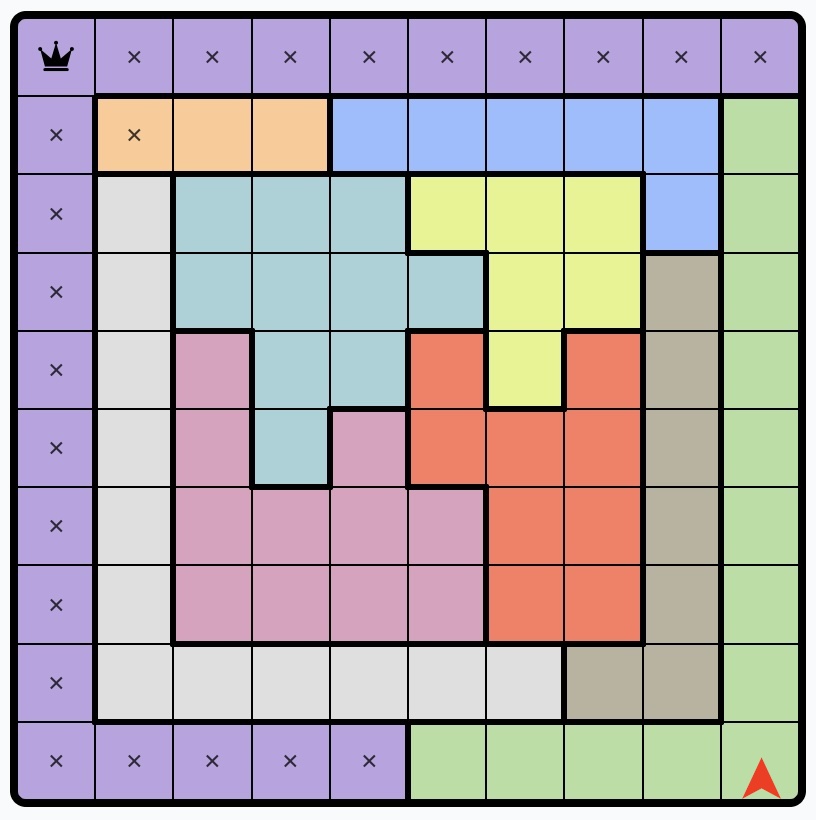
1. If there is a region that spans all possible squares of an entire row and an entire column, place a queen on the intersection of that row and column:
Because it’s one queen per column and one queen per row, these regions necessarily have a queen on the intersection of the only row and only column possible.
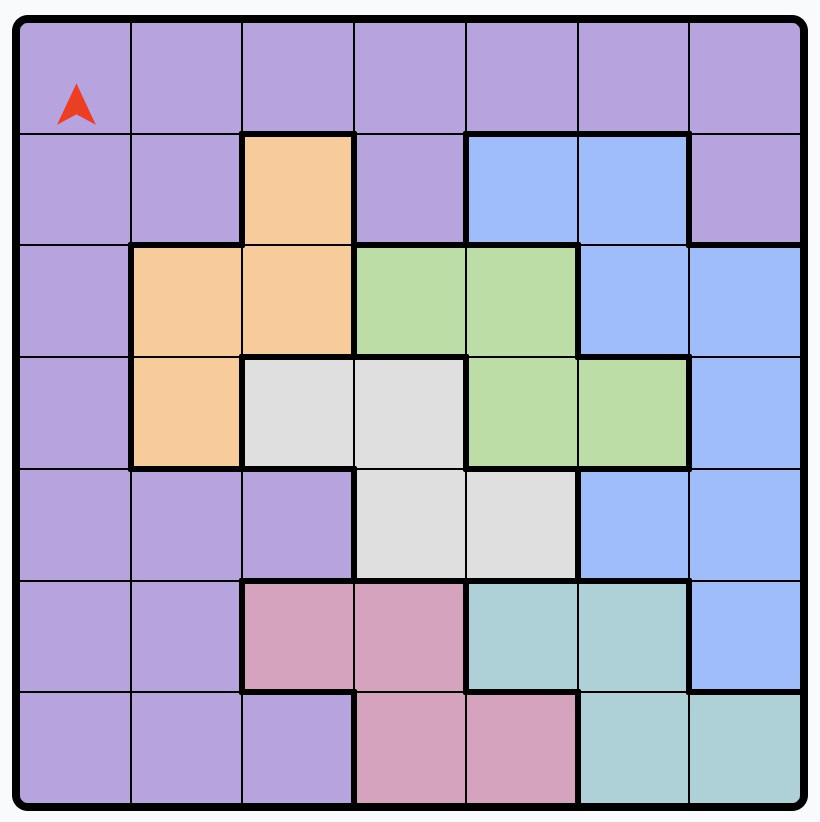
Initial board example:
After eliminating squares:
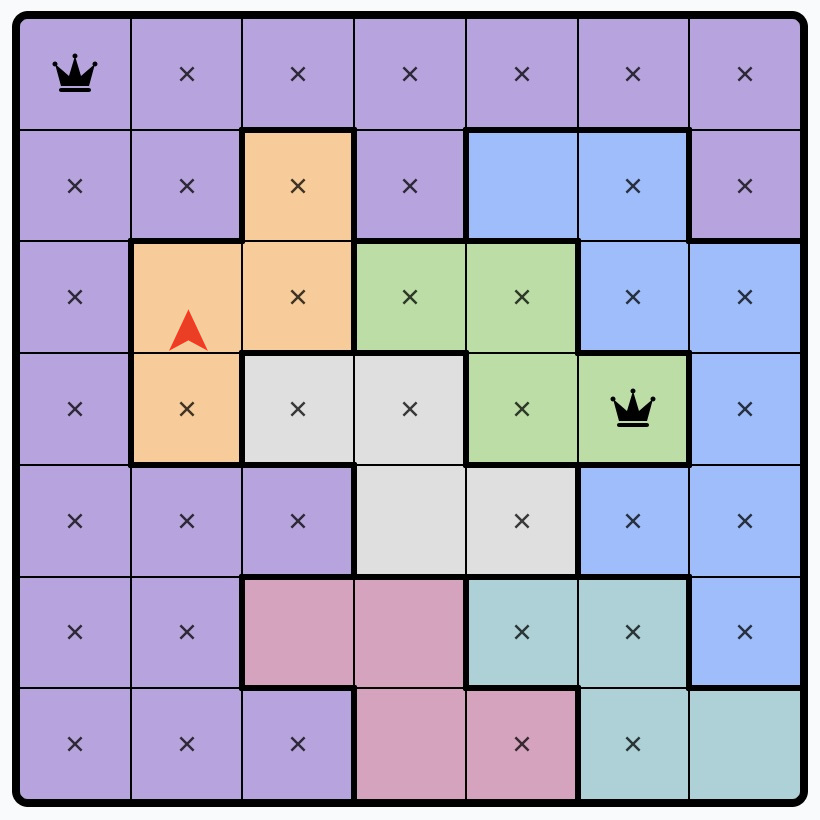
2. Place a queen on any region that has just one possible square:
Whether it’s a one-square-large region, or a region that has had all other squares Xed-out, there’s only one place to put a queen.
3. Place a queen on any row or column that has just one possible square:
Likewise with rows and columns.
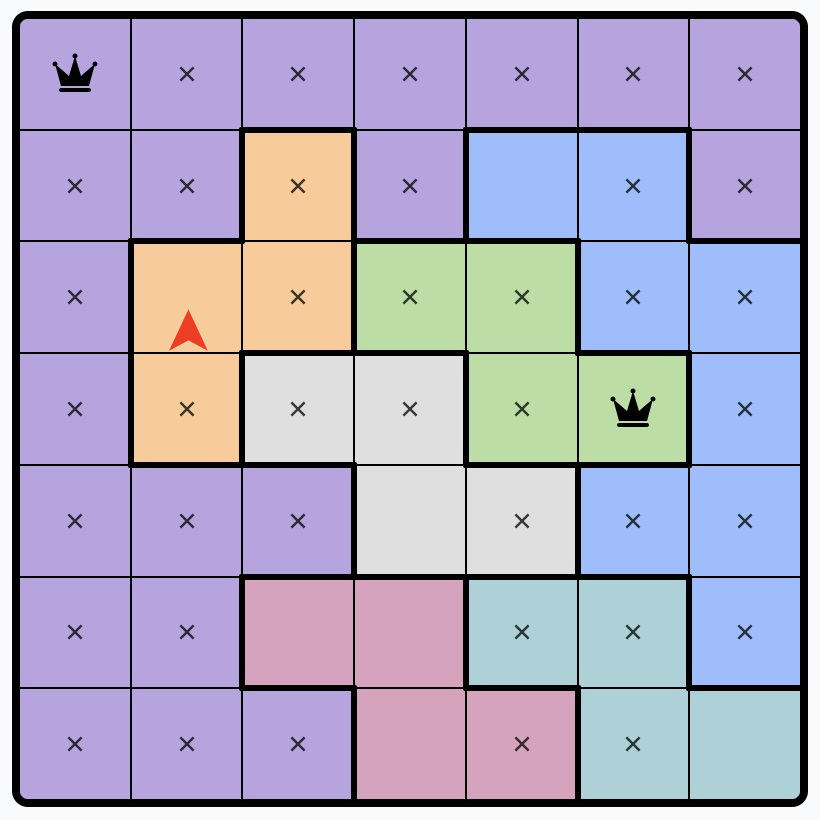
4. Place an X on squares that would block all the possible squares of a region:
Example: These two squares would block all of the green region’s squares due to covering three by proximity, and the fourth by row.
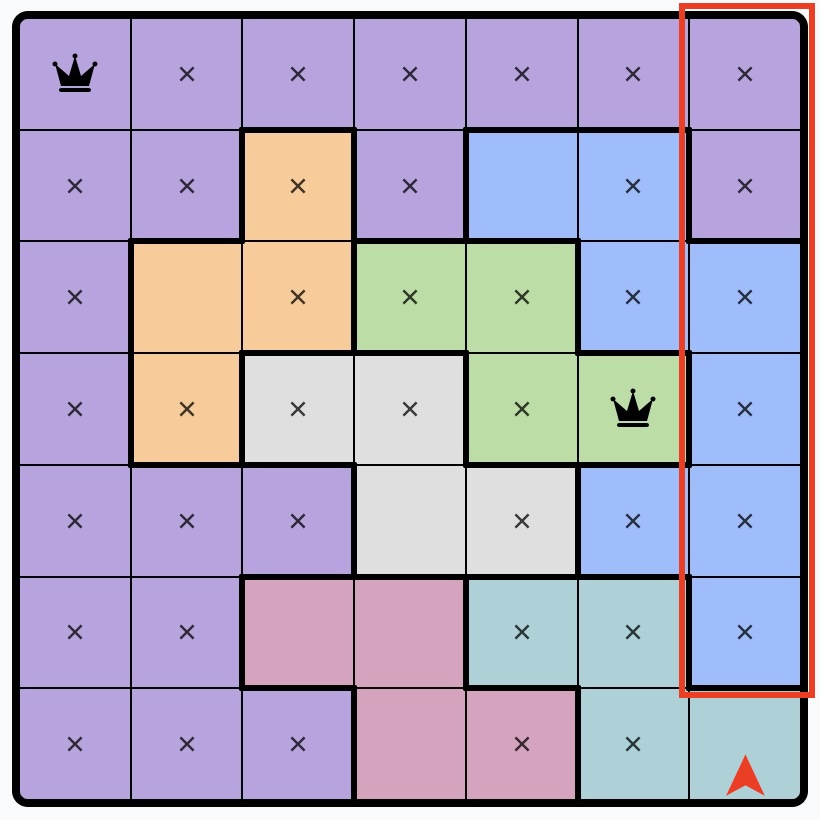
5. Place an X on squares that would block all the possible squares of a row or column:
Expanding on the previous step for row or column situations.
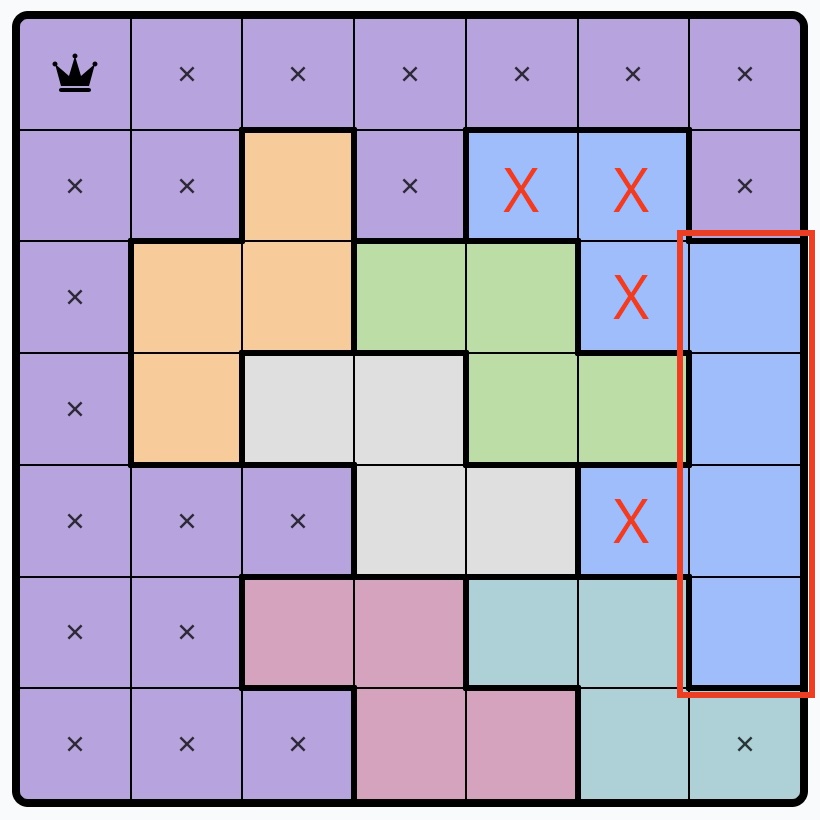
6. For any regions that span all possible squares of an entire row or column, place an X on squares in that region that are not on that row or column:
Each row or column needs one queen, so if a region spans all possible squares of a row or column, a queen must be there and not in the rest of the region.
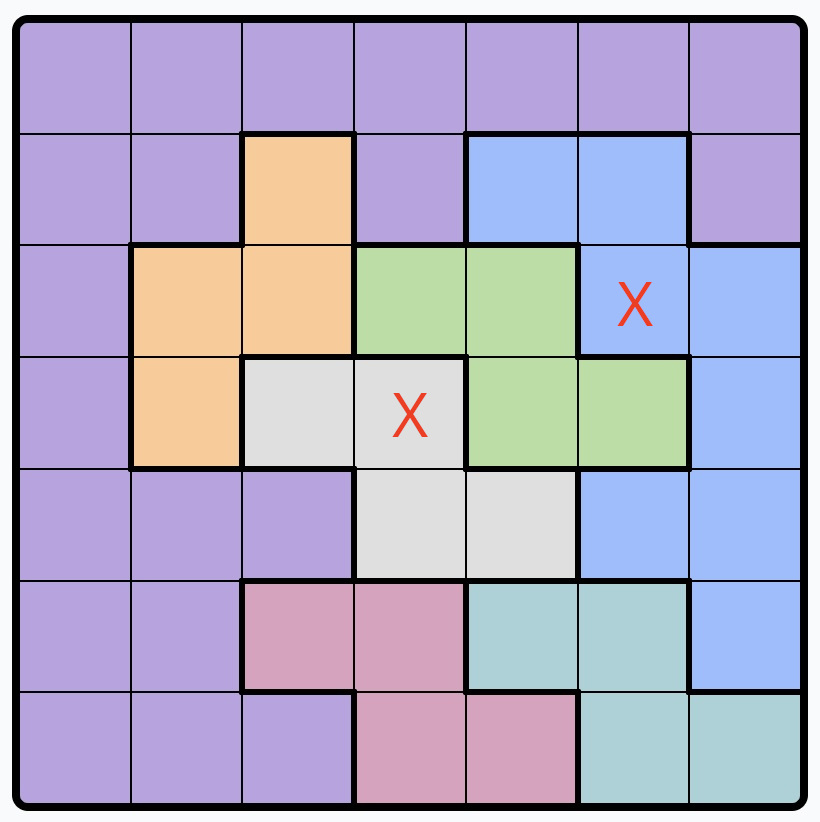
7. Place an X on the squares of regions that fall outside the rows or columns allocated to those regions:
Expanding on the previous step for multi-row or multi-column situations.
Example: These three columns must contain three queens in the three regions available. All other squares in these three regions can be safely eliminated.
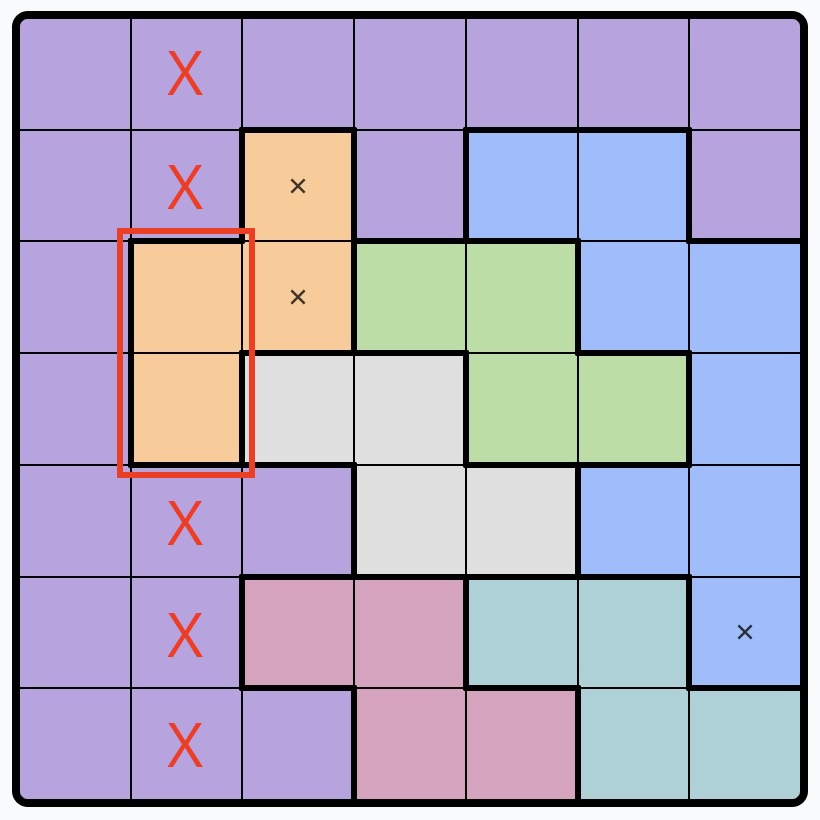
8. Any regions that have the only possible squares on one row or column, place an X on all other squares of that row or column:
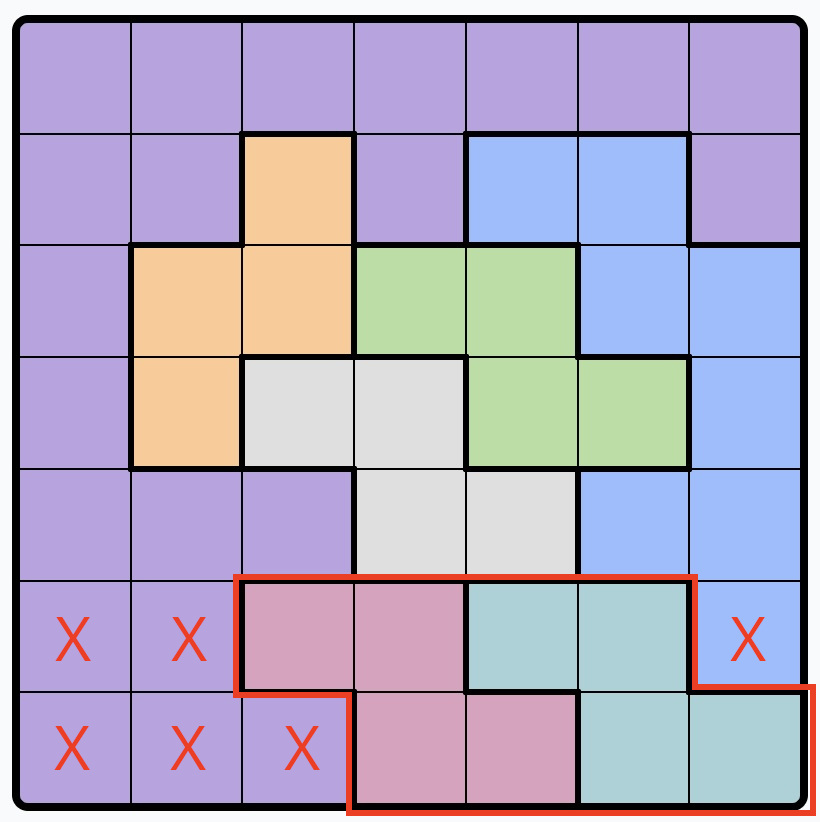
9. Place an X on squares that would overload the number of rows or columns allocated to regions:
Expanding on the previous step for multi-row or multi-column situations.
Example: These two regions have their only possible squares on two rows. Placing a queen on any other square of these two rows would make it impossible to have enough rows for these two regions. The same applies when there are three, four or more regions that have their only possible squares on three, four or more rows or columns. Bear in mind that the rows or columns might not be next to each other.
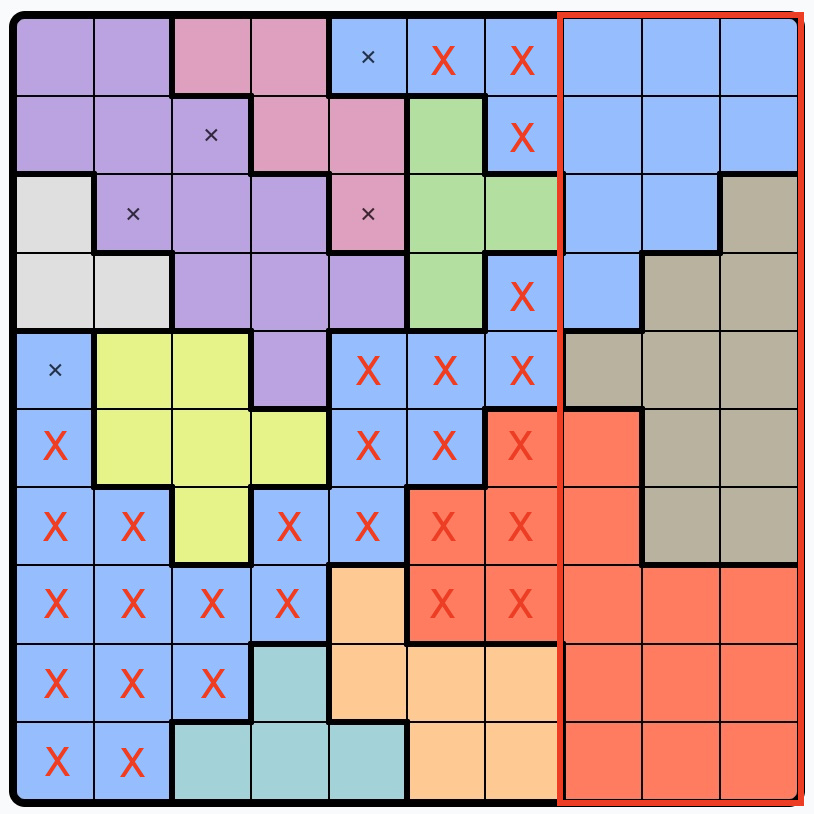
10. Repeat steps 1-9 until you solve the puzzle or have to guess:
The process of placing Xs will reduce possible squares in regions, and fewer possible squares in regions will reveal new squares to place an X or queen.
11. If you have to guess, start with the region(s) with the fewest possible squares
12. Guess the square that will eliminate the most possibilities:
If it’s a dead end, better to hit it early.
13. If at any point while guessing, you X-out all the squares of any region, back out until that region has selectable squares again, then put an X on the square you had guessed, and go back to step 11:
Process of elimination.
14. I’ll race you.
P.S. I’m aware that in my examples, I made some wrong placements. They’re examples.
P.P.S. I got an email asking for help with a Queens clone. If the above steps don’t have definitive boxes to mark with an X or a queen, then there are multiple solutions and you will have to guess. The version on LinkedIn is good about only having one solution.
P.P.P.S. LinkedIn doesn’t have an archive of past games, but Sami U. made a Queens clone that keeps a comprehensive archive of those LinkedIn games to play, as well as a fun level builder and community created levels, available here.
Share: